Click here and press the right key for the next slide.
(This may not work on mobile or ipad. You can try using chrome or firefox, but even that may fail. Sorry.)
also ...
Press the left key to go backwards (or swipe right)
Press n to toggle whether notes are shown (or add '?notes' to the url before the #)
Press m or double tap to slide thumbnails (menu)
Press ? at any time to show the keyboard shortcuts
An Objection to Decision Theory?
There are 90 balls in this urn.
30 of these balls are red.
The other balls are either black (all over) or yellow (all over).
One ball will be selected at random.
Please choose between:
option 1 : £100 if the ball is red, £0 otherwise
option 2 : £100 if the ball is black, £0 otherwise
Please choose between:
option A : £100 if the ball is red or yellow, £0 otherwise
option B : £100 if the ball is black or yellow, £0 otherwise
How to objection
1. State the finding.
2. State the axiom it contradicts.
3. Explain how the finding contradicts the axiom.
4. (If possible, explain why it is significant.)
5. Consider responses.
transitivity
For any A, B, C ∈ S: if A⪯B and B⪯C then A⪯C.
completeness
For any A, B ∈ S: either A⪯B or B⪯A
continuity
‘Continuity implies that no outcome is so bad that you would not be willing to take some gamble that might result in you ending up with that outcome [...] provided that the chance of the bad outcome is small enough.’
independence
roughly, if you prefer A to B then you should prefer A and C to B and C.
Steele & Stefánsson (2020, p. §2.3)
complication : different formalizations
‘Savage (1972, p. 21ff)'s Postulate 2, which he calls the "Sure-thing Principle"’
(Ellsberg, 1961, p. 649)
How to objection
1. State the finding.
2. State the axiom it contradicts.
3. Explain how the finding contradicts the axiom.
4. (If possible, explain why it is significant.)
5. Consider responses.
There are 90 balls in this urn.
30 of these balls are red.
The other balls are either black (all over) or yellow (all over).
One ball will be selected at random.
Please choose between:
option 1 : £100 if the ball is red, £0 otherwise
option 2 : £100 if the ball is black, £0 otherwise
Please choose between:
option A : £100 if the ball is red or yellow, £0 otherwise
option B : £100 if the ball is black or yellow, £0 otherwise
transitivity
For any A, B, C ∈ S: if A⪯B and B⪯C then A⪯C.
completeness
For any A, B ∈ S: either A⪯B or B⪯A
continuity
‘Continuity implies that no outcome is so bad that you would not be willing to take some gamble that might result in you ending up with that outcome [...] provided that the chance of the bad outcome is small enough.’
independence
roughly, if you prefer A to B then you should prefer A and C to B and C.
Steele & Stefánsson (2020, p. §2.3)
choice 1
£100 if Brazil win the world cup, £0 otherwise
£100 if France win the world cup, £0 otherwise
choice 2
£100 if Brazil or Ukraine win the world cup, £0 otherwise
£100 if France or Ukraine win the world cup, £0 otherwise
How to objection
1. State the finding.
2. State the axiom it contradicts.
3. Explain how the finding contradicts the axiom.
4. (If possible, explain why it is significant.)
5. Consider responses.
uncertainty vs risk
Sometimes people prefer less uncertainty.
Even when less uncertainty is more risky (Jia, Furlong, Gao, Santos, & Levy, 2020) ...
What if you inform people about the Ellsberg Paradox and show how it is costing them money?
What if you inform people about the Ellsberg Paradox and show how it is costing them money?
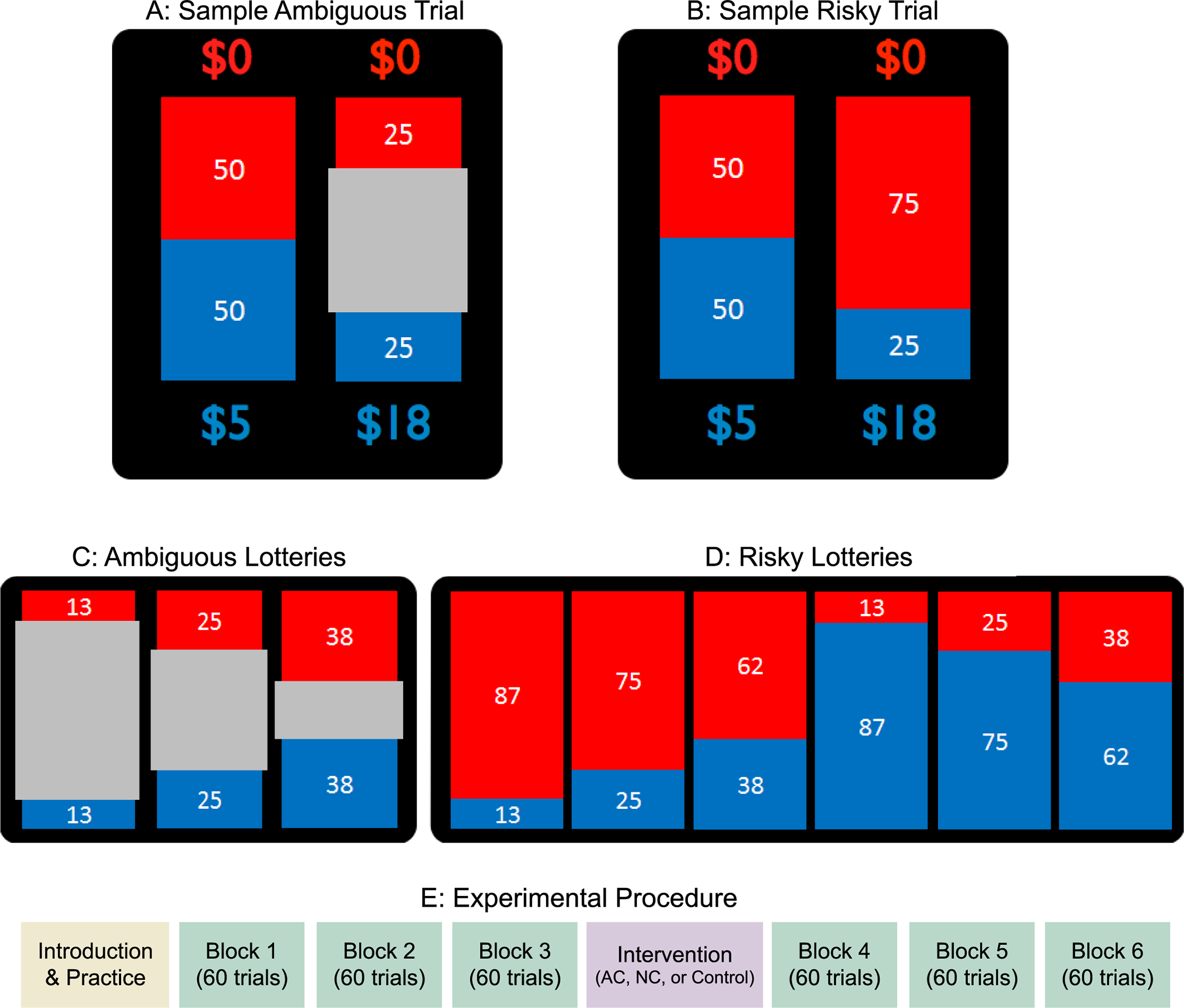
Jia et al. (2020, p. figure 1 (part))
What if you inform people about the Ellsberg Paradox and show how it is costing them money?
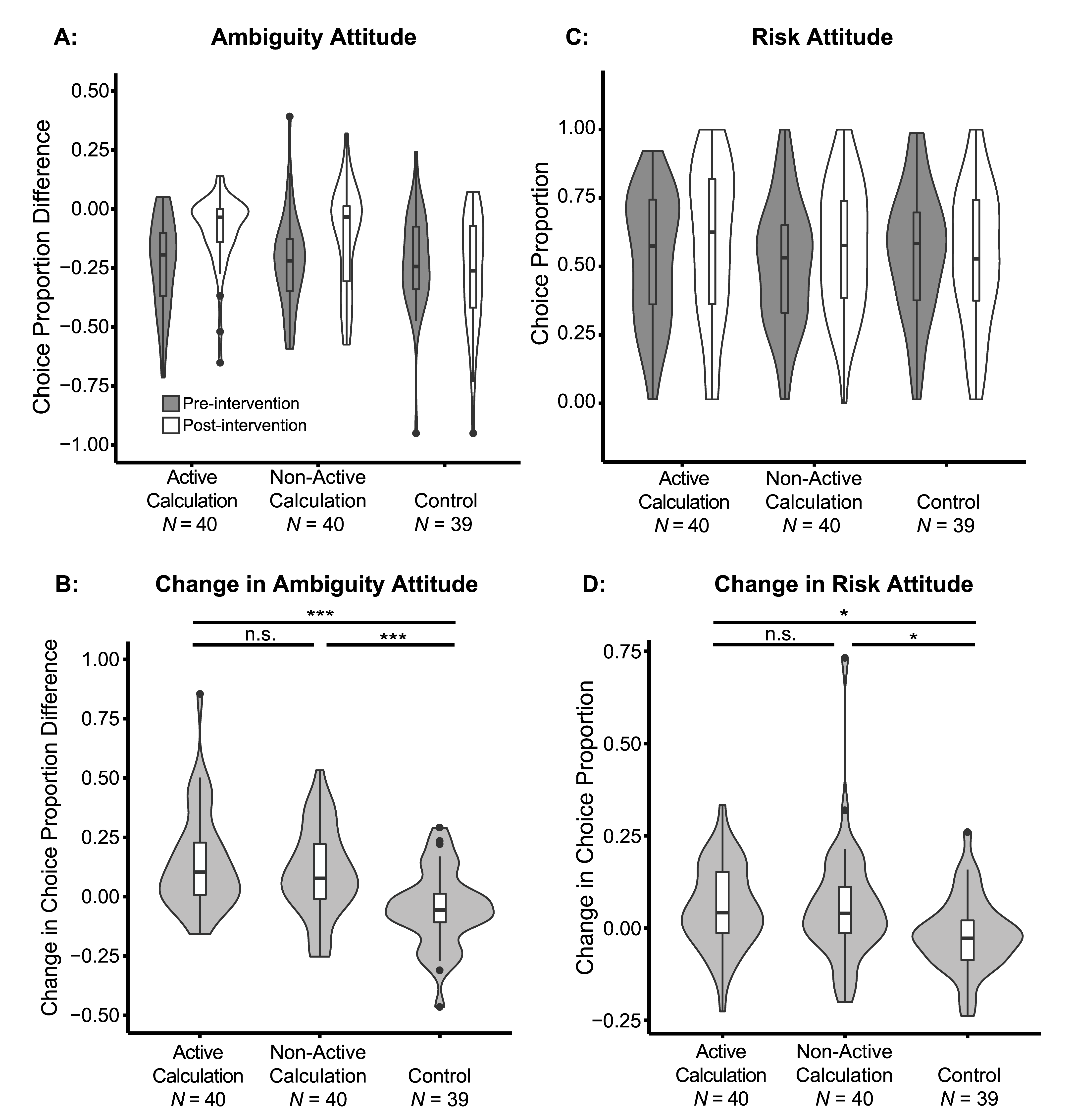
Jia et al. (2020, p. figure 4)
What if you inform people about the Ellsberg Paradox and show how it is costing them money?
‘awareness of the detrimental effect of ambiguity aversion [...] does reduce ambiguity aversion
BUT ‘ambiguity aversion [...] did not disappear
AND ‘participants also reduced their aversion to risk, suggesting inappropriate generalization of the learning to another irrelevant decision context.’
Jia et al. (2020)
How to objection
1. State the finding.
2. State the axiom it contradicts.
3. Explain how the finding contradicts the axiom.
4. (If possible, explain why it is significant.)
5. Consider responses.

response 1
‘both the predictive and normative use of the Savage or equivalent postulates might be improved by avoiding attempts to apply them in certain, specifiable circumstances where they do not seem acceptable’
Ellsberg (1961, p. 646)
response 2

‘we wish to find the mathematically complete principles which define “rational behavior” for the participants in a social economy, and to derive from them the general characteristics of that behavior’
von Neumann & Morgenstern, 1953 p. 31
‘the laws of decision theory [...] are not empirical generalisations about all agents. What they do is define what is meant ... by being rational’
(Davidson, 1987, p. 43)
Q1 : Are people who take a less ambiguous but more risky option actually irrational?
Q2 : Are there other applications of decision theory to which preferences to reduce ambiguity would be an objection?
(E.g. Jeffrey (1983, p. xi) construes decision theory as an ‘elucidation of the notions of subjective probability and subjective desirability’.)
How to objection
1. State the finding.
2. State the axiom it contradicts.
3. Explain how the finding contradicts the axiom.
4. (If possible, explain why it is significant.)
5. Consider responses.

a deeper understanding
Ellsberg Paradox
People’s preferences do not obey the independence axiom.
Normativist response: [shrugs]
Mandler’s Objection
‘Completeness applies to preference as choice, while transitivity applies to preference as a set of judgments of well-being. Convincing arguments for the axioms taken together cannot be assembled on either definition.’
(Mandler, 2001, p. 374; see also Mandler, 2005)
Decision theory and game theory have generated some amazing insights (see O’Connor, 2019, for example).
Apparently compelling objections abound.

How to objection
1. State the finding.
2. State the axiom it contradicts.
3. Explain how the finding contradicts the axiom.
4. (If possible, explain why it is significant.)
5. Consider responses.